The solera paradox
After I wrote about the ever-lasting Christmas beer, I read on the Wikipedia page for solera that soleras are used for vinegars, too, and some Italian producers then report the age of the entire solera as the age of their vinegar. The logic being that (a) "Italian labeling laws permit blended vinegar to be labeled with the age of the oldest vinegar in the blend" and (b) consumers are impressed. I woke up the next morning wondering ... what age should they have put? That is, if I were writing the law, what would I require them to state on the labelling?
Now, for the Swedish hundred-year beer only a single cask was used, and the general rule seemed to be to take off half the cask every second year, then refill with fresh beer. After a few hundred years of that, how old would the beer that you withdraw be? Well, obviously it would be a mix of different ages, so there's no single answer. But we could compute the average age of the contents, right? Or could we? What would the average mean?
One way to interpret it is this: imagine you take every single molecule, add up the number of years since that molecule was added to the cask, then divide by the number of molecules. Surely that would be a reasonable definition of "average age"? But, what would the answer be?
Note that there is a subtlety here. The age will be different at different times. Just before we withdraw half the contents, the average age will be quite different from after we refill the solera with 50% of new beer, of age 0. Then, one year later, the average age will obviously be one year higher, and so on. So which age should we choose? The obvious one to choose is the moment before we withdraw half the contents. After all, that will be the average age of the stuff we bottle.
I hadn't even gotten out of bed by the time I worked out that the formula would have to be, for a solera that had been maintained for an infinite number of years. Note that k here is not the year since we started, but the number of times we've removed half the contents.
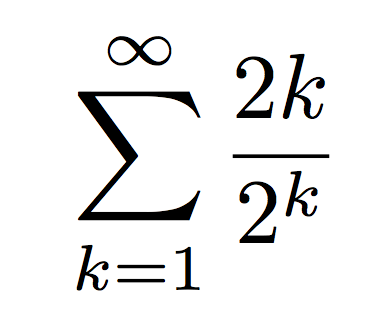
For anyone of a truly mathematical bent, that was probably obvious all along, and the rest of this blog post will be unnecessary. (The above formula contains the answer if you know how to deal with infinite series.) But this blog post is for the people who are not mathematicians, but rather normal people who want to know how old are the contents of the solera, and how we can claim to know the answer with any sort of certainty.
The formula above is actually shorthand for the following (first row), which then can easily be expanded into the two following rows. If you just walk through it I think you can easily see that the expansion is right. Note that 25 simply means 2 multiplied by itself 5 times, that is: 2 * 2 * 2 * 2 * 2.
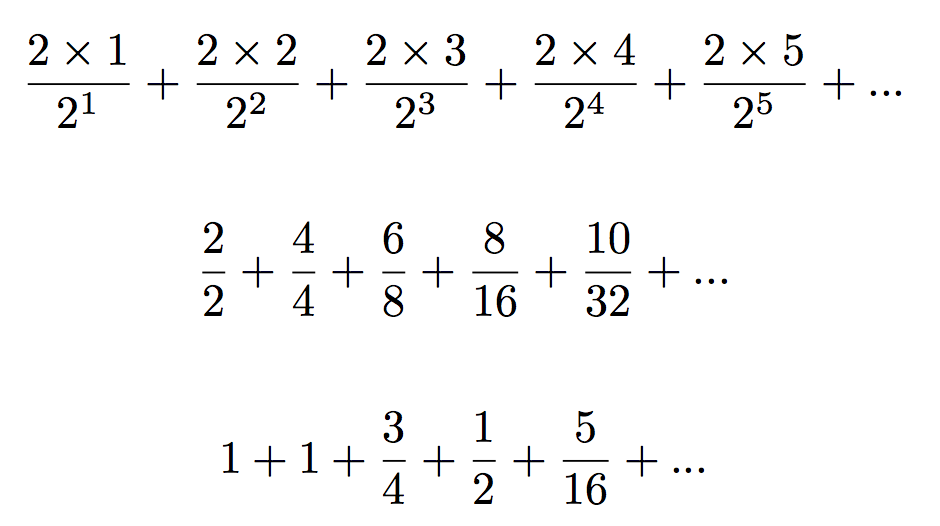
Looking at the second row above, what you notice is that the top part of the fraction doesn't grow very fast, but the bottom part does. By the time we get to k=10, the top will be 20, but the bottom will be 1024. At k=20 the top is 40 and the bottom is about a million. This is why the sum actually converges to a finite number, even though the series is infinite. As we go on, the later parts contribute less and less, and eventually they contribute so little as to be ignorable.
But what does the sum actually converge to? A mathematician could tell just from the initial formula, but the idea here is to make it blindingly obvious what the answer is, even to people who are not into maths. So, I'll make a table showing the result of the sum for each value of k, up to the point where I think everyone can see where this is headed. Let's say that's k=20, where the bottom part of the fraction is more than a million. To verify the first parts, just look up at the series above.
| 1 | 1.0 |
| 2 | 2.0 |
| 3 | 2.75 |
| 4 | 3.25 |
| 5 | 3.5625 |
| 6 | 3.75 |
| 7 | 3.859375 |
| 8 | 3.921875 |
| 9 | 3.95703125 |
| 10 | 3.9765625 |
| 11 | 3.9873046875 |
| 12 | 3.9931640625 |
| 13 | 3.99633789062 |
| 14 | 3.998046875 |
| 15 | 3.99896240234 |
| 16 | 3.99945068359 |
| 17 | 3.99971008301 |
| 18 | 3.99984741211 |
| 19 | 3.99991989136 |
| 20 | 3.99995803833 |
Well. I suppose at this point there's no doubt in anyone's mind about where this is headed. Obviously, this sum is going to wind up at 4.0. But that's bizarre! By the time the solera has been going for hundreds of years, how can the average age be so low as 4 years? That's nothing, yet there are molecules in here that have been floating around for much, much longer than that.
This result is surprising enough that it could make you doubt that the formula is right. According to this thing, the first half adds 1 year to the age. Which is weird, since although it's only half the solera, it's 2 years old. Even weirder is the fact that the second part, a quarter, also adds one year, even though it's four years old. Can this really be the correct formula?
To prove that it is, let's approach the issue from a completely different direction. Why not simulate the answer? If we divide the solera into, say, a million molecules, then simulate the fate of each of those, we should arrive at a fairly accurate answer. And since the way we do it is totaly different from what we did above, the answer should be reliable.
Below is the code. As you can see, we take a list of SIZE integers. Every year we increase all integers by one. Every other year we randomly shuffle the list, then throw away the second half, then replace it with zeroes. Then we repeat and repeat and repeat. The final bit counts how many occurrences we have of different ages.
import random
def average(numbers):
return sum(numbers) / float(len(numbers))
def age(solera):
return [age + 1 for age in solera]
def refill(solera):
random.shuffle(solera)
return solera[ : SIZE / 2] + [0] * (SIZE / 2)
def oldest(solera):
oldest = 0
for age in solera:
oldest = max(oldest, age)
return oldest
SIZE = 1000000
solera = [0] * SIZE
year = 0
YEARS = 1000
print year, average(solera)
while year < YEARS:
year += 1
solera = age(solera)
print year, average(solera)
year += 1
solera = age(solera)
print year, average(solera), oldest(solera)
if year < YEARS:
solera = refill(solera)
print year, average(solera)
ages = {}
for age in solera:
ages[age] = ages.get(age, 0) + 1
for age in range(0, 1000):
c = ages.get(age)
if c:
print age, c
If we run this, the output is as expected. Here's the final bit, years 982 to 1000.
982 3.999226 42 982 2.000634 983 3.000634 984 4.000634 40 984 2.00162 985 3.00162 986 4.00162 42 986 1.999584 987 2.999584 988 3.999584 44 988 1.999358 989 2.999358 990 3.999358 42 990 1.999156 991 2.999156 992 3.999156 44 992 1.99799 993 2.99799 994 3.99799 40 994 1.998202 995 2.998202 996 3.998202 42 996 2.000676 997 3.000676 998 4.000676 38 998 1.99735 999 2.99735 1000 3.99735 40
The year we refill the solera the average age of the contents is 4 before we refill. An hour or so later, the average age of the contents is 2, because we took away half the 4-year old beer, and replaced it with beer that's 0 years old. (This is why there are two entries for year 982, 984, ...) Then, the next year, the average age has gone up by one, since one year has passed and we've changed nothing. Then, when it's time to refill, we're back at 4.
So for my imaginary Italian law change we'd use the formula at the top for computing the age of the vinegar. Of course, it would have to be generalized to account for the fraction of vinegar that's replaced each time (it doesn't have to be half), and the number of years between each time. Doing so is left as an exercise for the reader. (I've always wanted to write that sentence myself.)
The extra number at the end of some of the lines above is the oldest part in the solera at that point. The age of that varies, as you can see, but it hovers around 40. On a couple of occasions it actually went as high as 52, but never above. If we look at the distribution of ages at the very end, we get this:
2 500000 4 250389 6 124974 8 62367 10 31080 12 15641 14 7780 16 3902 18 1929 20 979 22 486 24 251 26 122 28 54 30 22 32 13 34 6 36 2 38 2 40 1
Which corresponds fairly exactly to the theoretically predicted proportions. Of course, this is with 1,000,000 "molecules". What about in reality? How many molecules are there really? Well, the cask we read about was 150 liters. Computing the number of molecules is hard, because the number of them will vary with what type of molecule it is. And beer contains a crazy number of different molecules. By far the most of it, however, is water, so we'll make this easier for ourselves by assuming it's all water.
To work that out, we need to know how much 150 liters of water weighs. This is where the metric system comes into its own. By definition, one liter of water weighs one kilo. So that one's easy. But how many molecules are there in 150 kilos of water?
In physics this is calculated in a slightly odd way. You need to know the weight of one mole of your material, and the weight of one mole of water molecules is 18.0153 grams. The definition of a mole is that it has 6.022 * 1023 molecules (or atoms, depending on what you're working with). This number is known as Avogadro's number.
Anyway, we work out how many moles are in our 150 liters, then multiply that by Avogadro's number, and we have the number of molecules. I'm doing this calculation in grams, so 150 kilos is then 150,000 grams:

5 octillion molecules is a vast number. Five thousand million million million million molecules, in fact. So how many refills would it take on average to get rid of the last molecule of the original beer? To put it another way, how many times do we need to halve something before we're down to one five octillionth of the original? We need to find k so that 2k is about five octillion. That turns out to be 92.
Remember, though, that k is not the number of years, but the number of refills. If we refill every second year the oldest molecule will on average be 184 years old. So the oldest part of the hundred-year beer is in fact more than a hundred years old (assuming perfect mixing). But not quite ever-lasting.
Similar posts
The ever-lasting Christmas beer
In the early 17th century, walloon smiths were famous for their ironwork, and the Swedish kings therefore invited them to settle in Sweden
Read | 2014-12-21 11:51
Typed data in tolog
We've known for a long time that sooner or later we'd have to start supporting data types (numbers, dates, ...) in tolog, but so far we haven't done it
Read | 2006-05-10 23:17
How hops prevent infection
The increasingly inaccurately named series on yeast terminology continues with a post diving into how, exactly, hops prevent bacteria from infecting beer
Read | 2015-09-18 14:43
Comments
Pivní Filosof - 2014-12-24 10:44:55
I believe that on the label of some Sherry wines I've seen the legend "Min X years", indicating the oldest "batch" in the blend, but I wouldn't testify in a court of law and right now I feel too lazy to look it up to confirm
Ben - 2014-12-24 11:06:24
I have also seen a few excel charts to track soleras, including this one by Michael Tonsmeire (writer of "American Sour Beers" and editor/writer of the Mad Fermentationist blog: https://archive.org/details/SoleraAgingSpreadsheet
I like the "in homeopathic concentration" phrase.
Ed - 2014-12-24 14:09:09
Nice work!
Lars Marius - 2014-12-25 06:36:40
Ben: Yes, the actual maths involved are dead simple, so you could easily do it with a spreadsheet, too. I thought the interesting part would be to walk through why the calculation comes out the way it does. That phrase you liked is due to Harald Thunaeus, btw. :)
Jeffrey White - 2015-02-22 15:11:00
For those interested in the Solera process for themselves, Michael Tonsmeire, Author of American Sour Beer has made a solera age spreadsheet available to the public. I use it for my lambic and "American sour" soleras.
https://archive.org/details/SoleraAgingSpreadsheet