A family tree for kveik

Richard Preiss talking about his research at the farmhouse ale festival in Hornindal |
In 2016 I was contacted by Canadian researcher Richard Preiss. He wanted to do research on the kveik cultures I had collected, and after a while we agreed to set up a collaboration. Since then I've been sending a part of every farmhouse yeast I collect to Richard, and he has been keeping me up to date on his findings. Since this was ongoing research I haven't revealed his findings, but now a paper by Preiss, Tyrawa, and van der Merwe has been submitted to a journal, and everything is out in the open.
This is research that was mostly done last year, so not that many kveiks were included. They looked at the following:
| No | Name | Owner | Place | Region |
|---|---|---|---|---|
| 1 | Sigmund | Sigmund Gjernes | Voss | Hordaland, Norway |
| 3 | Stranda | Stein Langlo | Stranda | Sunnmøre, Norway |
| 4 | Muri | Bjarne Muri | Olden | Nordfjord, Norway |
| 5 | Raftevold | Terje Raftevold | Hornindal | Nordfjord, Norway |
| 6 | Lærdal | Dagfinn Wendelbo | Lærdal | Sogn, Norway |
| 8 | Sykkylven | Sigurd Johan Saure | Sykkylven | Sunnmøre, Norway |
| 7 | Granvin | Hans Haugse | Voss | Hordaland, Norway |
| 9 | Ebbegarden | Jens Aage Øvrebust | Stordal | Sunnmøre, Norway |
| 10 | Framgarden | Petter B. Øvrebust | Stordal | Sunnmøre, Norway |
| 16 | Simonaitis | Julius Simonaitis | Joniškelis | Aukštaitija, Lithuania |
The ID numbers are taken from my kveik registry, and as you can see quite a few kveiks are not included, because they were collected after the work had begun.
One thing we've found is that all of the yeast cultures contain more than one strain of yeast, except #3 Stranda, and that's probably because the yeast was very nearly dead, and only a single strain survived. The paper lists only one strain from #16 Simonaitis and #4 Muri, but NCYC found several. That there is more than one strain is what you would expect with yeast cultures that have not been purified.
Another surprise is that all of these yeasts, with one exception, are Saccharomyces cerevisiae. That is, ordinary top-fermenting beer/bread yeast. That's quite surprising, because there's no reason why they have to be, yet apparently they are. Except for #4 Muri, which was identified as a hybrid. (We'll return to that.)
However, although kveik turns out to be the same species as top-fermenting beer yeast, it doesn't have to be brewer's yeast. That is, it doesn't have to be yeast that has been domesticated, in the sense that humans have bred it to behave well in beer fermentation. It could still be wild yeast, that is, yeast that's basically still the same kind of yeast you find in nature, fermenting tree sap and fruit. The paper has some interesting light to shed on that question, so let's move on.

#3 Stranda as I got it |
The researchers looked at what flavours the kveiks produce, using gas chromatography, and this showed that the only ones that were phenolic (POF+) were #16 Simonaitis and #4 Muri. This is significant because while wild yeast is nearly always POF+, domesticated yeasts tend to be POF- (not phenolic). In other words, this is strong evidence that the kveiks are domesticated and not wild.
The temperature tolerance results are interesting: all the strains can grow at 40C, and most even at 42. It's not in the paper, but Richard Preiss found that the #1 Sigmund could also grow at 43. Of the normal lab yeasts, some couldn't even handle 35, and none could handle more than 40. Of course, the biggest difference is that many of the kveiks produce perfectly fine beer at 40. That result is not in the paper, but from personal experience.
This really sets the kveiks, and the Lithuanian yeast, apart from most other yeasts. I searched the Wyeast catalog and found no yeasts that were recommended for use above 30C. Yet I've had beer made with #1 Sigmund where the fermenter was pinned to 40C with a thermostat, and the resulting beer was clean as a bell.
Richard and the team also tested the yeasts for alcohol tolerance and nearly all handled 13%, and quite a few went as high as 16%. If we compare with the results in the Gallone paper we see that that's quite remarkable for beer yeast. Very likely this is because Norwegian farmers usually made quite strong beer.
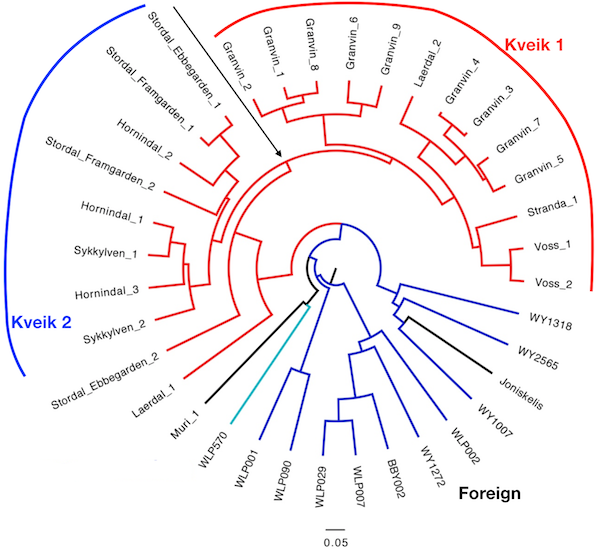
Phylogenetic tree of kveik strains from the paper (with annotations added by me) |
Now we come to the most telling result: the family tree of kveiks, as well as the Lithuanian yeast and some control yeasts. The genetic analysis finds a clean cut, with the foreign yeasts on one side, and the Norwegian ones on the other. (The red/blue split in the tree.) So the kveiks really look like they are a separate branch on the family tree of yeast. It's too early to conclude that Richard et al have found "Beer 3" (see the Gallone paper), but it's definitely interesting.
However, it doesn't end there. This summer, Richard sent me the tree diagram, saying he thought there were two types, which he was tentatively calling Kveik 1 and Kveik 2. I looked at it for a while and then nearly fell off my chair when I realized that these two groups had a nearly perfect correspondence with the local geography. All the Kveik 1 yeasts (except #3 Stranda) were from the boiled ale area south of the glacier, and all the Kveik 2 yeasts from the raw ale area north of the Jostedalen glacier. See the map here. In the tree above, the black arrow shows the point where Kveik 1 and 2 separate. In the map below the black line shows the glacier (and, at the two ends, mountains) separating the two areas.
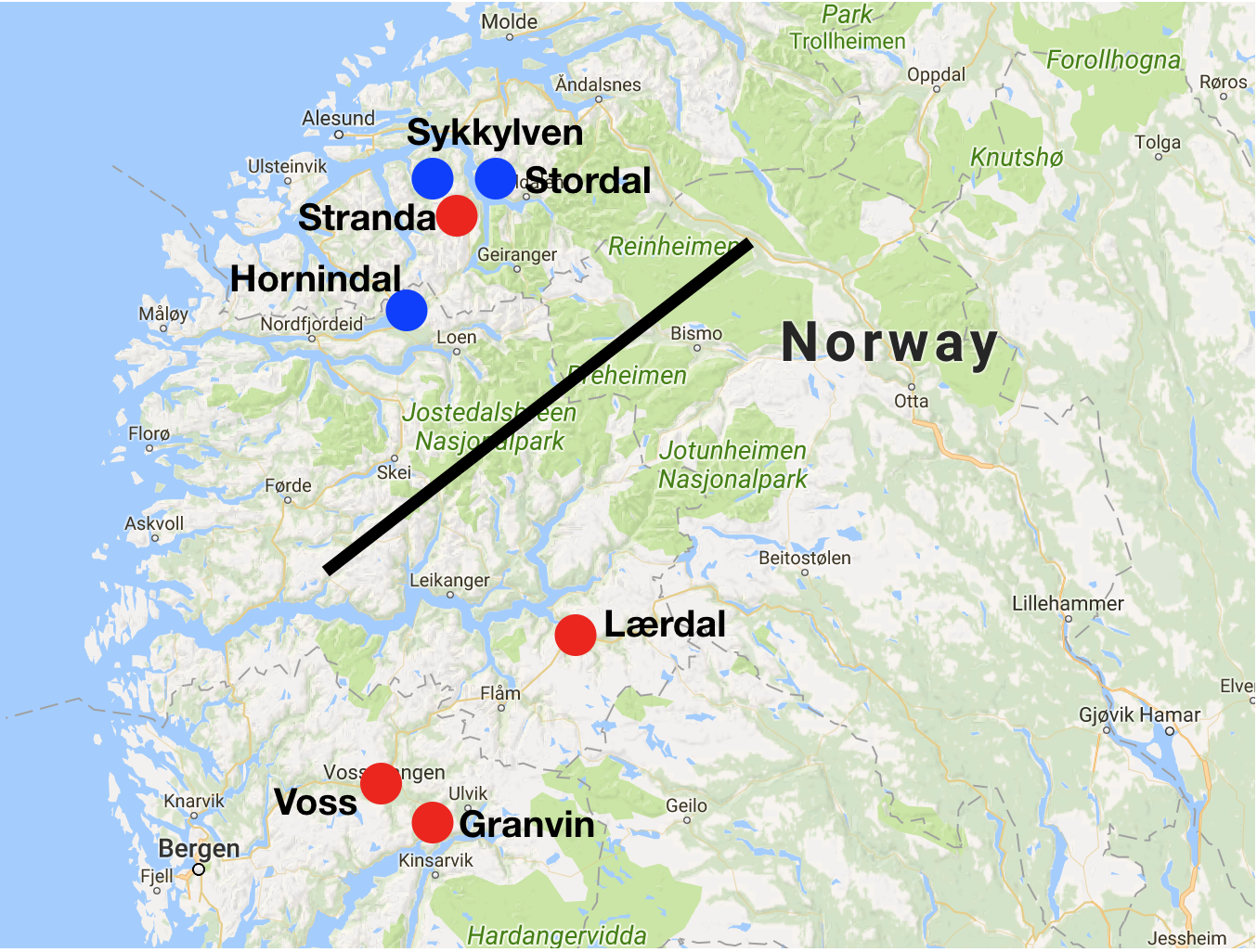
Yeast strains on the map |
Note that the results are better than the map makes them look, because each dot is more than a single strain. "Stordal" is four strains, for example. In total there's 8 Kveik 2 strains and 13 Kveik 1 strains, and only 1 of those 21 strains is in the "wrong" place. We need more data to be absolutely sure of this, but it's remarkable that the tree follows an already known divide. Richard has later added more yeasts to the tree (not published yet) and the results still hold up. So it's very promising.
At this point it's obvious that we are looking at domesticated yeasts, given that they are POF-, highly alcohol tolerant, have good attenuation, and all seem to be related even though they have been collected from many independent sources. Most of the owners mentioned in the table had never met each other when we collected their yeasts.
So have Norwegian farmers successfully managed to maintain and breed yeast cultures for centuries using basically nothing but wooden rings and sticks? We haven't proved it conclusively, but it sure looks that way. I really would love to see an analysis of when Kveik 1 and Kveik 2 split apart, and when they separated from the other yeasts. We'll have to wait a year or two for those results, though, if we ever get them.
These results repeat the findings from Gallone et al in two respects even if the analysis is of a completely different set of yeasts. Firstly, there seems to be a single ancestor, possibly in the near past. Secondly, geography is mirrored in the family tree. In this case fairly local geography, but still. That has to tell us something about the evolution and spread of yeast among brewers, but I'm still not sure what exactly.
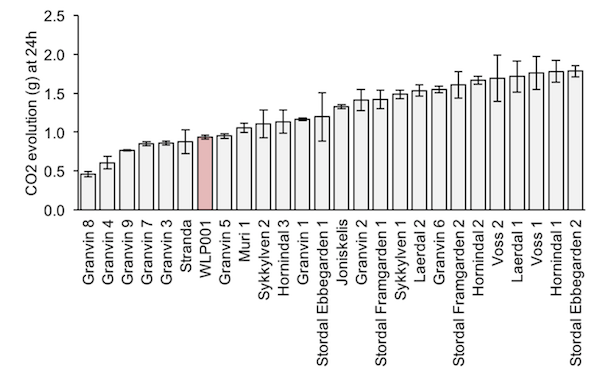
CO2 production in 24 hours (from the paper) |
Another finding that's interesting is that compared with the control 19 out of 25 kveiks fermented faster than it. That will surprise nobody who's seen these yeasts take off. They really do ferment astonishingly fast (0-7.5% in 33 hours is completely normal), and what's even more surprising is that you can drink the beer once fermentation is finished, or even before.
Further, they find that the kveiks have good attenuation (65-95%), and that they seem to make good use of maltotriose. Maltotriose is a sugar that appears in wort, but is rare in nature, so wild yeasts are not good at making use of it, but domesticated yeasts are. So this once again confirms that the kveiks are domesticated.
But what about Muri? It stands out a mile among the Norwegian yeasts, since it's a hybrid, it's POF+, and it produces a completely different aroma. So what's up with that? We'll look at that in the next posting.
Appendix
Earlier I wrote about another study which found several that kveik seemed to be several different species. The reason for that result seems to be that they used the ITS region of the genome to identify the species, and in this part of the genome the difference between Saccharomyces cerevisiae and Saccharomyces boulardii is just a single base pair. So it takes just a tiny mistake to put the yeast in the wrong species. That accounts for nearly all the differences between the earlier paper and this one, except for #6 Lærdal, and some Lithuanian ones that were not in this paper.
Some of the Lithuanian yeasts really are non-Saccharomyces, but since I don't have permission from the owners to do research on them I didn't send them to Richard. The results from this paper are based on more data, and so seem more likely to be the correct ones. The results in this paper also match the conclusions that NCYC came to, which is another reason to believe that this is the correct answer.
Unlike the Gallone paper this paper did not sequence the entire genome of the strains. So the genetic results in this paper are a bit more uncertain. The researchers have now gotten funding to sequence the whole genome of some strains, so more results will be forthcoming.
Similar posts
Where kveik comes from
I've written before about the kveik research paper by Preiss, Tyrawa, and van der Merwe
Read | 2018-09-12 16:27
Analysis of farmhouse yeast (kveik)
The Norwegian University of Science and Technology (NTNU) in Trondheim started doing research and courses on brewer's yeast a little over a year ago
Read | 2016-09-06 16:30
There is a Whole Family of European Farmhouse Yeasts
Six years ago, the paper that told us where kveik came from was published
Read | 2024-04-07 14:47
Comments
Marco - 2017-10-11 05:38:10
Fascinating! Learning about the history of brewing in Norway by reading your blog has been great, but seeing these figures really brings it home. There is clearly a rich story of human hands and beer making that has shaped this family tree. I await every new post!
Andrew - 2017-10-13 12:52:53
Hi, wondering if this has been published in a peer reviewed journal? Would love to see more methods.
Lars Marius Garshol - 2017-10-13 13:01:59
@Andrew: The paper (linked to near the top) has been submitted to a journal, yes. The paper has much more on methods than the blog post does. If you think the paper doesn't have enough detail on the methods I think you should email the authors. Their addresses are in the paper. I'm sure they would be happy to receive comments.
Fer - 2017-11-26 10:55:40
This is amazing. Every new result obtained makes this theme about kveik more fascinating. I brewed with the Sigmund's strain from The Yeast Bay and, although it started fermenting quite fast compared with other more typical yeasts, it took some more time than I have read around here. Apart from other factors (oxygen, number of cells,...) I guess this could be because the commercial yeast is only one strain while it appears that in Norway they use a mixed culture that would speed in a way the beginning of the fermentation.
I'm looking forward to see more results from the research
Thanks!
John McMullan - 2017-11-30 15:26:01
Considering the observed characteristics of these Kveik strains, I'm inclined to think they aren't necessarily Brewer's yeast. They sound more like Distiller's yeast. Finnish vodka yeast ferments well above 40¼C. Distiller's yeast are usually rapid fermenters too. Traditionally, Distillers' fermentations bypassed any temperature control, likely selecting for thermotolerant strains. Moreover, there is an association between temperature tolerance and alcohol tolerance in yeast. Non-ale strains of S. cerevisiae with higher temperature tolerances typically have higher alcohol tolerances too. So it isn't necessarily valid to separate these two Kveik traits. What is the history of home distilling in rural Norway?
John McMullan - 2017-11-30 17:18:39
@ Andrew. No, it isn't peer reviewed. I have quite a few issue with it myself, having just read it. It's certainly 'standing on shoulders' and not 'pushing yeast science'. It assumes for too much to get through peer review. All the historical claims are based on one publication, Norland (1969). As a scientist with an interest in Brewer's yeast, I have been following the Kveik story with interest. And I do take my hat off to Lars. However, I find the wild speculations of some concern, TBH. I guess some of us view things differently. The notion that Europeans domesticated Brewer's yeast is, itself, debatable. Brewing predates European civilisation. One hypothesis I'd entertain is that our ancestors who colonised Europe actually brought yeast cultures with them. They were already growing barley before that arrived. And I suspect that's the pattern that gets discovered, eventually. The idea that Brewer's yeasts were domesticated post-Industrial Revolution, or indeed, 'earlier in rural Norway' is probably a big, fat red herring. Such is the arrogance of Europeans ; ) The already-domesticated yeasts simply adapted to changing brewing environments. Without being more critical, it's up the garden path we're go...
Lars Marius Garshol - 2017-11-30 17:42:26
@John: I think this kind of raises the question of what we mean by "brewer's yeast" and "distiller's yeast". Especially given that you have to wonder where "distiller's yeast" comes from, since distillation hasn't actually been going on for that long, historically. But it may well be that kveik is more similar to yeasts used in distillation now than the commercial brewer's yeasts currently used. Historically, that would make a lot of sense.
Farmhouse fermentations also tended to be very hot, all over northern Europe (basically UK to the Urals, at least). And farmhouse fermentations began long, long before distillation. Two thousands years before, at the very least.
I'm not sure what you mean by "it isn't necessarily valid to separate these two Kveik traits". I don't know that anyone's doing that.
> What is the history of home distilling in rural Norway?
It came to Norway pretty late. It only started getting widely available in the 17th century, and rural distillation only really began 1-2 centuries later. It has been widely practiced, but always in areas that had already been brewing beer for a few millennia.
> All the historical claims are based on one publication, Norland (1969).
That's true, because it's the only thing published in English about Norwegian farmhouse ale. There are no other English sources to cite.
> The notion that Europeans domesticated Brewer's yeast is, itself, debatable.
Yes. However, I don't see that anyone's making that claim in this blog post or in this paper.
It is interesting, though, that Gallone et al 2016 find that the commercial brewing strains are so closely related they probably started diverging a few centuries ago. It kind of does point in the direction of Europeans domesticating brewer's yeast themselves, even if it's far from conclusive.
> 'earlier in rural Norway' is probably a big, fat red herring
I see Richard writes that kveik may have been domesticated separately from other brewing yeasts. Note that he does not claim it necessarily happened in Norway. There's no evidence (yet) to say where it happened, if it happened.
I don't see why it should be impossible, given the available timespans and the way farmhouse brewers have been using and collecting yeast. Brewing came to Europe millennia ago, and whether or not yeast strains came together with the knowledge of brewing, it would be surprising if there were zero examples of brewers in the millennia to follow domesticating yeast strains collected from nature by design or accident.
And if the Norwegians did this then 99% certainly they were not alone. If Norwegians did it, then probably so did everyone else. Probably the only difference is that we still have our yeast strains.
John McMullan - 2017-12-02 14:30:13
[I think this kind of raises the question of what we mean by "brewer's yeast" and "distiller's yeastÓ.] And Kveik? And every other yeast of cultural significance. The budding yeast, Sacharomyces cerevisiae, or ŌbakerÕs yeastÕ as itÕs commonly referred to in the literature. All S. cerevisiae strains share a common natural history. Some, through artificial selection, are better adapted for certain processes, while others have more than one use. Convergent evolution (due to ŌhotÕ fermentations/no temperature control) might explain the similarities between Kveik and distillerÕs yeast. What we do know is that yeast cultures evolve surprisingly quickly. The same yeast strain used in different breweries can diverge (acquire different qualities) over relatively short periods. These changes are not necessarily genetic either. Genetically, they might appear identical.
Distillation was common enough in Norway in the early 19th century for the Norwegian parliament to introduce an act to restrict its practice. Around the same time as potato became a popular crop in Norway (apparently encouraged by the British blocking grain shipments from Denmark, who were then allied to the French); about when Norwegian aquavit (flavoured potato spirit) appears on the scene. So almost 200 years. ThatÕs more than sufficient time for yeast cultures to adapt. I suspect Kveik goes back further, but what evidence is there? How can we be sure that contemporary cultures even compare with what was used in the past, beyond a generation of two? They werenÕt preserved in laboratories, unfortunately.
[Norland (1969)...There are no other English sources to cite.] Sources of evidence not written in English can be translated and cited in the normal way. Interesting as it is, folklore alone is not necessarily a reliable source of information. One thing that IÕm not sure whether you have mentioned is Bergen. Not only is it in the Kveik region of interest, itÕs famous for being an Hanse city therefore associated with a centuries-long trading link with Northern Germany. Did this have any influence on the local brewing culture? It might explain why some Kveik are more closely related to Kolsch strains, phylogenetically speaking. (Personally, I prefer Kveik over Kolsch. Kolsch puts the bland in bland.) It might explain too the curious origins of the Muri hybrid strain.
[Gallone et al 2016 find that the commercial brewing strains are so closely related they probably started diverging a few centuries ago.] I think that Ōlogical' hypothesis is inevitably biased by assumptions based on the molecular clock and by their samples (like most of these kind of studies). Had they used samples from pre-Industrial brewing houses or the home brewers before then (if they were available!), would similar patterns of relatedness have been presented? I donÕt see why not. In terms of phylogenies, be very critical. These trees are simply hypotheses, biased by samples, DNA quality, laboratory procedures (and the technicians carrying them out), platforms and, of course, analysis. Like any hypothesis, it needs to be tested with alternative evidence before concluding anything with confidence. I could probably engineer a 'new branch' on the brewing yeast tree with a little random luck, by starting a culture using baker's yeast from the cupboard, or from an oak tree, then select for traits desirable for brewing. Helped by the natural history of budding yeast - billions of cells grow in one small culture! Divide the culture and apply different conditions (selection pressures) to each subculture. It wouldn't take long to create a new brewing strain. Even a new 'branchÕ.
[A big, fat red herring.] That was meant for Europe generally, not just little Norway. The way I see it is this. Europeans didnÕt import and adopt brewing culture. Those who colonised Europe brought it along with them. Our hunter-gatherer ancestors were more than capable of fermenting wild fruit and vegetables as well as honey. The arrival of farming was a fortuitous development complementing a culture that was already practiced. Did they bring any strains with them? Who knows? I canÕt imagine how the mysterious properties of fermentation slurries were overlooked before the colonisation of Europe. It might gain support when sufficient data has accumulated, in a decade or two. It might not.
[Probably the only difference is that we still have our yeast strains.] But so too do the Belgians, English, Germans and others. It might be that their strains became fully domesticated sooner, partly due to the financial risks associated with industrialised brewing therefore the need to maintain the 'magic ingredient', yeast; whereas Kveik were slowly, if not partially, domesticated. Notwithstanding the apparent resistance to Ōleavening' society in rural Norway (it is a living museum in places), when you consider the ritual of Kveik brewing, the yeast log, after superstitiously stirring the wort with it then hanging it back up in the barn, attracts fruit flies carrying wild bakerÕs yeast (amongst other things) thus slowing the domestication process. The cultures replenished with some wild diversity. The same is probably true for preindustrial brewing elsewhere in Europe. It would be interesting to compare Kveik strains with local wild bakerÕs yeast, surviving on and beneath oak trees. They donÕt disperse very well at all. Significant distances probably depend on humans as agents of dispersal.
Richard Preiss - 2018-03-22 11:35:52
John - I apologize for being so late to this discussion, but I appreciate the commentary. We have take this commentary and other useful criticism into consideration in the revision of our manuscript, especially with regard to supplying more historical and contemporary context and references for Kveik use in brewing. Additionally, we have added more of the Beer strains used in the Gallone study to our (admittedly limited) fingerprint analysis, as well as distilling, wine and bread yeasts, to rule these out as origins of the hypothetical Kveik off-branch.
I agree with you in principle that S. cerevisiae phylogeny is always going to be somewhat confounded by convergent evolution. In fact, I would love to see a study attempt domestication of yeast through the directed evolution chemostat experiments that are being performed in a number of research labs. I think this would help us understand domestication better than just looking at the genetics of yeasts which have already been domesticated! Presumably, some of the specific genetic changes that confer domestication traits (POF loss of function, MAL gene duplication, etc) should be reproducible in such a study.
Mike Whitehead - 2019-05-02 03:11:51
Why are domestic yeasts more often POF-? I can think of three hypotheses:
a) ascertainment bias (they were POF- before domestication, and therefore more likely to be cultured) b) phylogenetic conservatism (most domestic yeast descend from a POF- common ancestor) or c) loss of POF is a repeated feature of yeast domestication
Do we know which is the case?
Lars Marius Garshol - 2019-05-02 06:04:29
@Mike:
Regarding a): This could be the case. As far as I know wild yeast is pretty much universally POF+, but I don't know enough to say that none were ever POF-.
Regarding b): This is probably part of the answer. Just look at the Beer 1 family, which makes up a huge part of today's beer yeasts. According to the Gallone et al paper, the Beer 1 ancestor turned POF- very early in its domestication. The Beer 2 family is largely POF+ (maybe even 100%). But there are many beer yeasts in the Mixed (later renamed Beer/baking) group, too.
Regarding c): It does seem to be a repeated feature of domestication, since 4 out of 8 beer yeasts in the Mixed group also are POF-.
Mike Whitehead - 2019-05-03 01:44:11
@Lars:
As so often is the case in biology, the answers are multifarious and complicated! Cheers.
Joshua Bugge - 2019-05-08 00:35:26
I really like the practical knowledge of how to brew with these yeast, but I have some serious concerns with the scientific research. Not to be too critical, but a few other comments have also raised concerns about the research and its conclusions.
I have concerns with the methods, but the most obvious problem I see in the conclusions are that Kveik strains represent their own lineage distinct from other brewers yeast. That is not the case with the reported results. The authors own phylogenetic tree absolutely shows that Kveik strains form their own group nested WITHIN all the other yeasts tested, not separate from all other tested strains. This means they are in the same clade as the sampled brewers yeast and there is no way to say they form a separate lineage from other brewer's yeast.
Kveik is still unique since all the strains in red are more related to each other than any other brewer's yeast, but they are not a separate lineage from brewers yeast in general. Just another group within brewer's yeast. Phylogenetic trees are read from the nodes not the tips. https://evolution.berkeley.edu/evolibrary/article/0_0_0/phylogenetics_02
As far as the discussion about distiller's yeast, knowing that Kveik form their own clade within brewer's yeast, I would be curious to see where the tested distiller's strains fall. There are a lot of possible scenarios, so I will wait to see the data and results.
Lars Marius Garshol - 2019-05-08 18:57:43
@Joshua: I guess this is a question of exactly how to word the finding. I agree kveik forms a separate group within the existing groups of brewer's yeast, and that's what this blog post was meant to say.
As for the methods, I recommend looking at this blog post http://www.garshol.priv.no/blog/391.html which reproduces the result with more exact methods.
Richard Preiss - 2019-05-10 17:49:28
@Joshua
We too recognized the fingerprinting approach taken initially as limiting, which is why we moved to the whole genome sequencing approach used in the published manuscript (https://www.frontiersin.org/articles/10.3389/fmicb.2018.02137/full) The manuscript was peer-reviewed by three rather well-known yeast geneticists and improved quite significantly thanks to their help.
In the paper we find that kveik are indeed nested within the Beer 1 group, but the story isn't so simple as kveik being an early offshoot of Beer 1. We found evidence through haplotype phasing that kveik may be a hybrid of a Beer 1 parental lineage and a currently unknown parental lineage (fig 2b). The population structure analysis of fig 3 helps to strengthen our argument that kveik are indeed genetically distinct, even if they are nested within the Beer 1 group. We are moving forward with WGS of more kveik, as well as long read sequencing to confirm and improve the phasing approach to better clarify kveik's genomic origins.
Also of note, Gallone 2016 found that most distiller's and bread yeasts fall within what they call the Mixed clade.
qq - 2019-05-21 21:13:25
@Mike Whitehead :
It's complicated, but bear in mind that there are all sorts of biases going on here. For instance, what you see in a Fermentis/Wyeast/White Labs catalogue may not be terribly representative of real-world brewery yeasts - maybe half the British yeast in the old Brewlab lists had descriptions that hinted at POF+ness, albeit weak in some cases.
But also you can imagine selection going on - if someone was starting brewing or had lost their yeast, you can imagine the advice being to go get some from the guy with the clean yeast rather than the guy with the old-style clovey yeast, in the same way that modern homebrewers are often advised to start with WLP001/1056/US-05.
Aside from direct mutation, you also have the fluidity of yeast genomes to contend with - for instance it looks like the hefe yeasts are a POF- kolschy yeast that stole a bit of saison DNA to become POF+ again.
(also Lars not all Group 2's are POF+, WLP026, allegedly from Marstons, is an example of a POF- one)